Análisis factorial

DefiniciónEditar

El modelo intenta explicar un conjunto de p observaciones en cada uno de n individuos con un conjunto de k factores comunes (F) donde hay menos factores por unidad que observaciones por unidad (k<p). Cada individuo tiene k factores comunes propios, y éstos se relacionan con las observaciones a través de la matriz de carga factorial ( L ∈ R p × k {\displaystyle L\in \mathbb {R} ^{p\times k}}.

${displaystyle L\in \mathbb {R} ^{p\times k}}$

), para una única observación, según x i , m – μ i = l i , 1 f 1 , m + ⋯ + l i , k f k , m + ϵ i , m {\displaystyle x_{i,m}-\mu _{i}=l_{i,1}f_{1,m}+\dots +l_{i,k}f_{k,m}+\epsilon _{i,m}}.

$Donde ϵ i , m {\displaystyle \epsilon _{i,m}}$

${displaystyle \\silon _{i,m}}$

es el término de error estocástico no observado con media cero y varianza finita, y μ i {\displaystyle \mu _{i}}

$mu _{i}$

es la media de la observación para la i-ésima observación.

En notación matricial

X – M = L F + ϵ {\displaystyle X-\mathrm {M} =LF+\epsilon }

$X-\mathrm {M} =LF+\epsilon$

donde la matriz de observación X ∈ R p × n {\displaystyle X\Nen \Nmathbb {R} ^{p\times n}}

${{descripción de X en \mathbb {R} ^{p\times n}}$

, la matriz de factores F ∈ R k × n {{descripción de F en \mathbb {R} ^{k\times n}}

${{displaystyle F en \mathbb {R} ^{k\times n}}$

, matriz de términos de error ϵ ∈ R p × n {{displaystyle \silon \ en \mathbb {R} ^{p\times n}}

${{displaystyle \epsilon \in \mathbb {R} ^{p\times n}}$

y la matriz media M ∈ R p × n {{displaystyle \mathrm {M}} \in \mathbb {R} ^{p\times n}}

${desde el estilo de visualización de los mates} \in \mathbb {R} ^{p\times n}}$

donde el elemento i, m es simplemente μ i {\displaystyle \mu _{i}}

$mu _{i}$

También impondremos las siguientes suposiciones sobre F {{displaystyle F}}

$F$

F y ϵ {\displaystyle \epsilon }
$\epsilon$

son independientes.
E ( F ) = 0 {\displaystyle \mathrm {E} (F)=0} (F)=0}
$mathrm {E} (F)=0$

; donde E es la Expectativa
C o v ( F ) = I {\displaystyle \mathrm {Cov} (F)=I}
$\mathrm {Cov} (F)=I$

donde Cov es la matriz de covarianza, para asegurar que los factores no están correlacionados, e I es la matriz identidad.

Supongamos que C o v ( X – M ) = Σ {\displaystyle \mathrm {Cov} (X-\mathrm {M} )=\Sigma }

${displaystyle \mathrm {Cov} (X-\mathrm {M} )=Sigma }$

. Entonces Σ = C o v ( X – M ) = C o v ( L F + ϵ ) , {\displaystyle \Sigma =\mathrm {Cov} (X-\mathrm {M} )=\mathrm {Cov} (LF+\epsilon ),\\,

${displaystyle \\NSigma =\mathrm {Cov} (X-\mathrm {M} )=\mathrm {Cov} (LF+\epsilon ),}$

y por tanto, de las condiciones impuestas a F anteriormente,

Σ = L C o v ( F ) L T + C o v ( ϵ ) , {\displaystyle \Sigma =L\mathrm {Cov} (F)L^{T}+\mathrm {Cov}(\epsilon ),\},

${displaystyle \Sigma =L\mathrm {Cov} (F)L^{T}+\mathrm {Cov} (\epsilon ),}$

o, poniendo Ψ = C o v ( ϵ ) {\displaystyle \Psi =\mathrm {Cov} (\epsilon )}

$\Psi =\mathrm {Cov} (\epsilon )$

, Σ = L L T + Ψ . {\displaystyle \Sigma =LL^{T}+\Psi .\\},}

$Sigma =LL^{T}+\Psi .\},$

Nota que para cualquier matriz ortogonal Q, si establecemos L ′ = L Q {\displaystyle L^{\prime }=LQ}

${desde el estilo L^{prime }=LQ}$

y F ′ = Q T F {{desde el estilo F^{prime }=Q^{T}F}

${displaystyle F^{prime }=Q^{T}F}$

, los criterios de ser factores y cargas factoriales siguen siendo válidos. Por lo tanto, un conjunto de factores y cargas factoriales es único sólo hasta una transformación ortogonal.

EjemploEditar

Supongamos que un psicólogo tiene la hipótesis de que hay dos tipos de inteligencia, la «inteligencia verbal» y la «inteligencia matemática», ninguna de las cuales se observa directamente. Las pruebas de la hipótesis se buscan en las puntuaciones de los exámenes de cada una de las 10 áreas académicas diferentes de 1000 estudiantes. Si cada estudiante se elige al azar de una gran población, entonces las 10 puntuaciones de cada estudiante son variables aleatorias. La hipótesis del psicólogo puede decir que, para cada uno de los 10 campos académicos, la puntuación promediada sobre el grupo de todos los estudiantes que comparten algún par de valores comunes para las «inteligencias» verbal y matemática es alguna constante por su nivel de inteligencia verbal más otra constante por su nivel de inteligencia matemática, es decir, es una combinación lineal de esos dos «factores». Los números de una asignatura concreta, por los que se multiplican los dos tipos de inteligencia para obtener la puntuación esperada, se postulan en la hipótesis como los mismos para todos los pares de niveles de inteligencia, y se denominan «carga factorial» para esta asignatura. Por ejemplo, la hipótesis puede sostener que la aptitud media prevista del alumno en el campo de la astronomía es

{10 × la inteligencia verbal del alumno} + {6 × la inteligencia matemática del alumno}.

Los números 10 y 6 son las cargas factoriales asociadas a la astronomía. Otras materias académicas pueden tener diferentes cargas factoriales.

Dos estudiantes que se supone que tienen idénticos grados de inteligencia verbal y matemática pueden tener diferentes aptitudes medidas en astronomía porque las aptitudes individuales difieren de las aptitudes medias (predichas anteriormente) y por el propio error de medición. Tales diferencias conforman lo que se llama colectivamente el «error» -un término estadístico que significa la cantidad por la que un individuo, tal como se mide, difiere de lo que es el promedio para o predicho por sus niveles de inteligencia (ver errores y residuos en estadística)

Los datos observables que entran en el análisis factorial serían 10 puntuaciones de cada uno de los 1000 estudiantes, un total de 10.000 números. A partir de los datos hay que inferir las cargas factoriales y los niveles de los dos tipos de inteligencia de cada alumno.

Modelo matemático del mismo ejemploEditar

En lo que sigue, las matrices se indicarán mediante variables indexadas. Los índices «sujetos» se indicarán mediante letras a {\displaystyle a}

$a$

, b {\displaystyle b}

$b$

y c {\displaystyle c}

$c$

, con valores que van desde 1 {\displaystyle 1}

$1$

hasta p {\displaystyle p}

$p$

que es igual a 10 {\displaystyle 10}

$10$

en el ejemplo anterior. Los índices «factoriales» se indicarán con las letras p {\displaystyle p}

$p$

, q {\displaystyle q}

$q$

y r {\displaystyle r}

$r$

, con valores que van desde 1 {\displaystyle 1}

$1$

a k {\displaystyle k}

$k$

que es igual a 2 {\displaystyle 2}

en el ejemplo anterior. Los índices de «instancia» o «muestra» se indicarán con las letras i {\displaystyle i}

$i$

, j {\displaystyle j}

$j$

y k {\displaystyle k}

$k$

, con valores que van desde 1 {\displaystyle 1}

$1$

a N {\displaystyle N}

$N$

. En el ejemplo anterior, si una muestra de N = 1000 {\displaystyle N=1000}

${displaystyle N=1000}$

los estudiantes participaron en el p = 10 {\displaystyle p=10}

${displaystyle p=10}$

exámenes, el i {\displaystyle i}

$i$

la puntuación del tercer estudiante para el a {\displaystyle a}

$a$

tercer examen viene dada por x a i {\displaystyle x_{ai}

$x_{ai}$

. El objetivo del análisis factorial es caracterizar las correlaciones entre las variables x a {\displaystyle x_{a}}.

$x_{a}$

de las cuales la x a i {\displaystyle x_{ai}}

$x_{ai}$

son una instancia particular, o conjunto de observaciones. Para que las variables estén en igualdad de condiciones, se normalizan en puntuaciones estándar z {\displaystyle z}

$z$

: z a i = x a i – μ a σ a {\displaystyle z_{ai}={\frac {x_{ai}-\mu _{a}}{sigma _{a}}}}

$z_{ai}={frac {x_{ai}-\mu _{a}}{sigma _{a}}$

donde la media muestral es:

μ a = 1 N ∑ i x a i {\displaystyle \mu _{a}={tfrac {1}{N}{suma _{i}x_{ai}}

$mu _{a}={tfrac {1}{N}}suma _{i}x_{ai}$

y la varianza muestral viene dada por:

σ a 2 = 1 N – 1 ∑ i ( x a i – μ a ) 2 {\displaystyle \sigma _{a}^{2}={tfrac {1}{N-1}}\suma _{i}(x_{ai}-\mu _{a})^{2}

${displaystyle \\Nsigma _{a}^{2}={tfrac {1}{N-1}}{suma _{i}(x_{ai}-\mu _{a})^{2}$

El modelo de análisis factorial para esta muestra en particular es entonces:

Z 1 , i = ℓ 1 , 1 F 1 , i + ℓ 1 , 2 F 2 , i + ε 1 , i ⋮ ⋮ ⋮ z 10 , i = ℓ 10 , 1 F 1 , i + ℓ 10 , 2 F 2 , i + ε 10 , i {\displaystyle {\begin{matrix}z_{1,i}&&ell _{1,1}F_{1,i}&&ell _{1,2}F_{2,i}&&\varepsilon _{1,i}\\\\\Nde los puntos &&\Nde los puntos &&\vdots &&\vdots \z_{10,i}&&ell _{10,1}F_{1,i}&&ell _{10,2}F_{2,i}&&\varepsilon _{10,i}\end{matrix}}}

${{comenzar{matriz}}z_{1,i}={célula _{1,1}F_{1,i}+{célula _{1,2}F_{2,i}+{varepsilon _{1,i}{círculo}},i}=\ell _{10,1}F_{1,i}+\ell _{10,2}F_{2,i}+\\i}varepsilon _{10,i}$

o, más sucintamente:

z a i = ∑ p ℓ a p F p i + ε a i {\displaystyle z_{ai}=\a suma _{p}ell _{ap}F_{pi}+\a varepsilon _{ai}}

$z_{ai}=suma _{p}ell _{ap}F_{pi}+{varepsilon _{ai}$

donde

F 1 i {{displaystyle F_{1i}}
${{displaystyle F_{1i}}$

es el i{{displaystyle i}

$i$

la «inteligencia verbal» del estudiante,
F 2 i {\displaystyle F_{2i}}
${{displaystyle F_{2i}}$

es la i{displaystyle i}

$i$

la «inteligencia matemática» del estudiante,
ℓ a p {\displaystyle \ell _{ap}}
$\ell _{ap}$

son las cargas de los factores para el a {displaystyle a}

$a$

th sujeto, para p = 1 , 2 {\displaystyle p=1,2}

${displaystyle p=1,2}$

.

En notación matricial, tenemos

Z = L F + ε {\displaystyle Z=LF+\varepsilon }

${{displaystyle Z=LF+\varepsilon }$

Obsérvese que al duplicar la escala en la que la «inteligencia verbal» -el primer componente de cada columna de F{{displaystyle F}

$F$

– se mide, y simultáneamente la reducción a la mitad de las cargas factoriales para la inteligencia verbal no hace ninguna diferencia en el modelo. Por lo tanto, no se pierde ninguna generalidad al suponer que la desviación estándar de los factores para la inteligencia verbal es de 1 {\displaystyle 1}

$1$

. Lo mismo ocurre con la inteligencia matemática. Además, por razones similares, no se pierde ninguna generalidad al suponer que los dos factores no están correlacionados entre sí. En otras palabras: ∑ i F p i F q i = δ p q {\displaystyle \sum _{i}F_{pi}F_{qi}=\delta _{pq}}

$suma _{i}F_{pi}F_{qi}=delta _{pq}$

donde δ p q {\displaystyle \delta _{pq}}

$delta _{pq}$

es el delta de Kronecker ( 0 {\displaystyle 0}

$0$

cuando p ≠ q {\displaystyle p\neq q}

$p\Nnecesidad de q$

y 1 {\displaystyle 1}

$1$

cuando p = q {\displaystyle p=q}

$p=q$

).Se supone que los errores son independientes de los factores: ∑ i F p i ε a i = 0 {\displaystyle \sum _{i}F_{pi}\varepsilon _{ai}=0}

$suma _{i}F_{pi}\varepsilon _{ai}=0$

Nota que, como cualquier rotación de una solución es también una solución, esto dificulta la interpretación de los factores. Ver desventajas más adelante. En este ejemplo concreto, si no sabemos de antemano que los dos tipos de inteligencia no están correlacionados, entonces no podemos interpretar los dos factores como los dos tipos diferentes de inteligencia. Incluso si no están correlacionados, no podemos decir qué factor corresponde a la inteligencia verbal y cuál a la inteligencia matemática sin un argumento externo.

Los valores de las cargas L

$L$

, las medias μ {displaystyle \mu }

$\mu$

, y las varianzas de los «errores» ε {\displaystyle \varepsilon }

$varepsilon$

deben estimarse dados los datos observados X {\displaystyle X}

$X$

y F {\displaystyle F}

$F$

(la suposición sobre los niveles de los factores es fija para un F {\displaystyle F} dado

$F$

). El «teorema fundamental» puede derivarse de las condiciones anteriores: ∑ i z a i z b i = ∑ j ℓ a j ℓ b j + ∑ i ε a i ε b i {\displaystyle \sum _{i}z_{ai}z_{bi}=\sum _{j}ell _{aj}\bj}+\sum _{i}varepsilon _{ai}varepsilon _{bi}}

${displaystyle \\_sum _{i}z_{ai}z_{bi}={sum _{j}ell _{aj}ell _{bj}+{sum _{i}{varepsilon _{ai}{varepsilon _{bi}}$

El término de la izquierda es el ( a , b ) {\diseño (a,b)}

$(a,b)$

-término de la matriz de correlación (a p × p {\displaystyle p\times p}

$p\a veces p$

matriz derivada como el producto de la p × N {displaystyle p\a veces N}

$matriz de observaciones estandarizadas con su transposición) de los datos observados, y su p {\displaystyle p}$ $p$

los elementos diagonales serán 1 {\displaystyle 1}

$1$

s. El segundo término de la derecha será una matriz diagonal con términos menores que la unidad. El primer término de la derecha es la «matriz de correlación reducida» y será igual a la matriz de correlación excepto por sus valores diagonales que serán menores que la unidad. Estos elementos diagonales de la matriz de correlación reducida se denominan «comunalidades» (que representan la fracción de la varianza en la variable observada que es explicada por los factores): h a 2 = 1 – ψ a = ∑ j ℓ a j ℓ a j {{displaystyle h_{a}^{2}=1-\psi _{a}={suma _{j}{ell _{aj}}

${{displaystyle h_{a}^{2}=1-\psi _{a}=suma _{j}{aj}{aj}$

Los datos de la muestra z a i {{displaystyle z_{ai}}

$z_{ai}$

no obedecerán, por supuesto, exactamente a la ecuación fundamental dada anteriormente debido a errores de muestreo, inadecuación del modelo, etc. El objetivo de cualquier análisis del modelo anterior es encontrar los factores F p i {\displaystyle F_{pi}}

$F_{pi}$

y las cargas ℓ a p {\displaystyle \ell _{ap}}

$\ell _{ap}$

que, en cierto sentido, dan un «mejor ajuste» a los datos. En el análisis factorial, el mejor ajuste se define como el mínimo del error cuadrático medio en los residuos fuera de la diagonal de la matriz de correlación: ε 2 = ∑ a ≠ b 2 {\displaystyle \varepsilon ^{2}={suma _{neq b}{left^{2}}.

${displaystyle \varepsilon ^{2}=suma _{a\neq b}\left^{2}$

Esto equivale a minimizar los componentes no diagonales de la covarianza del error que, en las ecuaciones del modelo tienen valores esperados de cero. Esto debe contrastarse con el análisis de componentes principales que busca minimizar el error cuadrático medio de todos los residuos. Antes de la llegada de los ordenadores de alta velocidad, se dedicaba un esfuerzo considerable a encontrar soluciones aproximadas al problema, en particular a estimar las comunalidades por otros medios, lo que simplifica considerablemente el problema al producir una matriz de correlación reducida conocida. Esta matriz se utilizó para estimar los factores y las cargas. Con la llegada de los ordenadores de alta velocidad, el problema de minimización puede resolverse de forma iterativa con la velocidad adecuada, y las comunalidades se calculan en el proceso, en lugar de ser necesarias de antemano. El algoritmo MinRes es especialmente adecuado para este problema, pero no es el único medio iterativo para encontrar una solución.

Si se permite que los factores de la solución estén correlacionados (como en la rotación ‘oblimin’, por ejemplo), entonces el modelo matemático correspondiente utiliza coordenadas sesgadas en lugar de coordenadas ortogonales.

Interpretación geométricaEditar

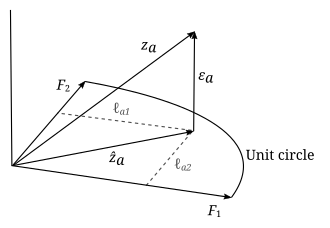Interpretación geométrica de los parámetros del Análisis Factorial para 3 encuestados a la pregunta «a». La «respuesta» está representada por el vector unitario z a {\displaystyle \mathbf {z} _{a}}

$\mathbf {z} _{a}$ mathbf {z} que se proyecta sobre un plano definido por dos vectores ortonormales F 1 _{1}}

$\mathbf {F} _{1}$ mathbf {F}

y F 2 {\displaystyle \mathbf {F} _{2}} _{2}}

$\mathbf {F} _{2}$ mathbf {F} 2}

. El vector de proyección es z ^ a {\displaystyle {\hat {\mathbf {z}} }}_{a}}

${hat {\mathbf {z}} y el error ε a.$ ${\boldsymbol {\varepsilon }}$

es perpendicular al plano, por lo que z a = z ^ a + ε a {\displaystyle \mathbf {z} _{a}={que {{mathbf {z}} { {{símbolo de negrita}} + {{varepsilon}} {{a}}

$\mathbf {z} _{a}={\hat {\mathbf {z} }}_{a}+{\boldsymbol {\varepsilon }}_{a}$ …que no es un símbolo de la muerte, sino que es un símbolo de la muerte. {{a}}+{{símbolo de negrita}} {{varepsilón}}

. El vector de proyección z ^ a {\displaystyle {\hat {\mathbf {z}} }}_{a}}

${{hat {\mathbf {z}} puede representarse en términos de los vectores factoriales como z ^ a = ℓ a 1 F 1 + ℓ a 2 F 2 {\displaystyle {\hat {\mathbf {z}} {{a}}={a1}{mathbf}{a1}{a2} 1+2. _{2}}$ ${que {{mathbf {z}} {{a}}={célula}{a1}{mathbf}{f}{a1} 1+2. _{2}$

. El cuadrado de la longitud del vector de proyección es la comunalidad: | | z ^ a | 2 = h a 2 {\displaystyle |||{hat {\mathbf {z} }}_{a}||^{2}=h_{a}^{2}}

${{displaystyle}} {{hat {\mathbf}} {z} }}_{a}||^{2}=h_{a}^{2}}$

. Si otro vector de datos z b {\displaystyle \mathbf {z} _{b}}

$\mathbf {z} _{b}$

fueron trazados, el coseno del ángulo entre z a {\displaystyle \mathbf {z} _{a}} _{a}}

$\mathbf {z} _{a}$ mathbf {z}

y z b {\displaystyle \mathbf {z} _{b} _{b}}

$\mathbf {z} _{b}$

sería r a b {{displaystyle r_{ab}}

$r_{ab}$

: el ( a , b ) {\displaystyle (a,b)}

$(a,b)$

-entrada en la matriz de correlación. (Adaptado de la Fig. 4.3 de Harman)

Los parámetros y las variables del análisis factorial pueden tener una interpretación geométrica. Los datos ( z a i {\displaystyle z_{ai}}

$z_{ai}$

), los factores ( F p i {\displaystyle F_{pi}}

$F_{pi}$ ) y los errores ( ε a i {\displaystyle \varepsilon _{ai}}

$varepsilon _{ai}$

) pueden ser vistos como vectores en un N {displaystyle N}

$N$

-dimensionales del espacio euclidiano (espacio muestral), representados como z a {\displaystyle \mathbf {z} _{a}}

$mathbf {z}$

, F j {\displaystyle \mathbf {F} _{j}} _{j}}

${{displaystyle \\_mathbf {F}}$

y ε a {\displaystyle {\boldsymbol {\varepsilon }_{a}}

${{símbolo de negrita}_{silon}}$

respectivamente. Como los datos están estandarizados, los vectores de datos son de longitud unitaria ( | | z a | | = 1 {\displaystyle |||mathbf {z} _{a}||=1}

${displaystyle |||mathbf {z} _{a}||=1}$

). Los vectores factoriales definen un k {\displaystyle k}

$k$

-dimensional subespacio lineal (es decir, un hiperplano) en este espacio, en el que los vectores de datos se proyectan ortogonalmente. Esto se deduce de la ecuación del modelo z a = ∑ j ℓ a j F j + ε a {\displaystyle \mathbf {z} _{a}=suma _{j} {{aj}}mathbf {{F}} + símbolo de negrita.

${displaystyle }{mathbf}{z}} _{a}=suma _{j}ell _{aj}{mathbf {F} y la independencia de los factores y los errores: F j ⋅ ε a = 0 {\displaystyle \mathbf {F} {{j}\cdot {\boldsymbol {\varepsilon }}_{a}=0}$

${displaystyle \mathbf {F}}$ Se trata de un hiperplano que se encuentra en la parte superior de la pantalla y que se encuentra en la parte inferior de la pantalla. En el ejemplo anterior, el hiperplano es sólo un plano de 2 dimensiones definido por los dos vectores del factor. La proyección de los vectores de datos sobre el hiperplano viene dada por z ^ a = ∑ j ℓ a j F j {\displaystyle {\hat {\mathbf {z}} {{a}}=suma _{j} {{aj}}mathbf {{F}} _{j}}

${displaystyle} {{hat} {{mathbf}} {{z}} {{a}}=suma _{j} {{aj}}mathbf {{F}}$

y los errores son vectores desde ese punto proyectado hasta el punto de datos y son perpendiculares al hiperplano. El objetivo del análisis factorial es encontrar un hiperplano que sea un «mejor ajuste» a los datos en algún sentido, por lo que no importa cómo se elijan los vectores factoriales que definen este hiperplano, siempre que sean independientes y estén en el hiperplano. Somos libres de especificarlos como ortogonales y normales ( F j ⋅ F q = δ p q {\displaystyle \mathbf {F} F q = p q = p q = p q = p q = p q = p q = p q = p q = p q = p q = p q = p q = p q = p q. _{q}=\\Ndelta _{pq}}

${{displaystyle \mathbf {F}} ...y el resto del mundo... _{q}=\delta _{pq}}$

) sin pérdida de generalidad. Después de encontrar un conjunto adecuado de factores, también se pueden rotar arbitrariamente dentro del hiperplano, de modo que cualquier rotación de los vectores del factor definirá el mismo hiperplano, y también será una solución. En consecuencia, en el ejemplo anterior, en el que el hiperplano de ajuste es bidimensional, si no sabemos de antemano que los dos tipos de inteligencia no están correlacionados, no podemos interpretar los dos factores como los dos tipos diferentes de inteligencia. Incluso si no están correlacionados, no podemos saber qué factor corresponde a la inteligencia verbal y cuál a la inteligencia matemática, o si los factores son combinaciones lineales de ambas, sin un argumento externo.

Los vectores de datos z a {\displaystyle \mathbf {z} _{a}}

$\mathbf {z} _{a}$ mathbf {z} _{a}

tienen longitud unitaria. Las entradas de la matriz de correlación para los datos vienen dadas por r a b = z a ⋅ z b {\displaystyle r_{ab}=\mathbf {z} r_{ab}=mathbf {z} {{b}} _{b}}

$r_{ab}={mathbf} {z} ...y no se puede hacer nada.$

. La matriz de correlación puede interpretarse geométricamente como el coseno del ángulo entre los dos vectores de datos z a {\displaystyle \mathbf {z} _{a}}

$mathbf {z}$

y z b {\displaystyle \mathbf {z} _{b}} _{b}}

$\mathbf {z} _{b}$ _{b}

. Los elementos diagonales serán claramente 1 {\displaystyle 1}

$1$

s y los elementos fuera de la diagonal tendrán valores absolutos menores o iguales a la unidad. La «matriz de correlación reducida» se define como r ^ a b = z ^ a ⋅ z ^ b {\displaystyle {\hat {r}_{ab}={hat {\mathbf {z} {{a}} {{hat} {{mathbf}} {{z}} }}_{b}}

${qué}_r}_{ab}={qué} {{mathbf}{z}} {{a}} {{cdot}} {{hat}} {{mathbf}} {{z}} {}_{b}$

El objetivo del análisis factorial es elegir el hiperplano de ajuste de tal manera que la matriz de correlación reducida reproduzca la matriz de correlación lo más posible, a excepción de los elementos diagonales de la matriz de correlación que se sabe que tienen valor unitario. En otras palabras, el objetivo es reproducir con la mayor precisión posible las correlaciones cruzadas de los datos. En concreto, para el hiperplano de ajuste, el error cuadrático medio en los componentes fuera de la diagonal

ε 2 = ∑ a ≠ b ( r a b – r ^ a b ) 2 {{displaystyle \varepsilon ^{2}={suma _{a\neq b}{left(r_{ab}-{hat {r}_{ab}\right)^{2}}

${displaystyle \varepsilon ^{2}={suma _{a\neq b}{izquierda(r_{ab}-{hat {r}}{derecha)^{2}$

se quiere minimizar, y esto se consigue minimizándolo con respecto a un conjunto de vectores factoriales ortonormales. Se puede ver que

r a b – r ^ a b = ε a ⋅ ε b {{displaystyle r_{ab}-{{hat {r}_{ab}={boldsymbol {{varepsilon }}{a}{cdot {{varepsilon }}{b}

$r_{ab}-{hat {r}_{ab}={boldsymbol {{varepsilon}}_{a}{cdot {\boldsymbol {{varepsilon}}$

El término de la derecha es sólo la covarianza de los errores. En el modelo, la covarianza de los errores se declara como una matriz diagonal y, por lo tanto, el problema de minimización anterior producirá, de hecho, un «mejor ajuste» al modelo: Se obtendrá una estimación de la muestra de la covarianza del error que tiene sus componentes fuera de la diagonal minimizados en el sentido del cuadrado medio. Se puede ver que desde el z ^ a {\displaystyle {hat {z}_{a}}

${hat {z}_{a}$

son proyecciones ortogonales de los vectores de datos, su longitud será menor o igual que la longitud del vector de datos proyectado, que es la unidad. El cuadrado de estas longitudes son los elementos diagonales de la matriz de correlación reducida. Estos elementos diagonales de la matriz de correlación reducida se conocen como «comunalidades»: h a 2 = | | z ^ a | 2 = ∑ j ℓ a j 2 {\displaystyle {h_{a}^{2}=||{hat {\mathbf {z} {{a}}||^{2}=suma _{j}{célula _{aj}^{2}

${{displaystyle{h_{a}}^{2}=|{hat{mathbf}{z}} {{a}}||^{2}=suma _{j}{célula _{aj}^{2}$

DefiniciónEditar

EjemploEditar

Modelo matemático del mismo ejemploEditar

Interpretación geométricaEditar

Deja una respuesta Cancelar la respuesta