La eficiencia de un algoritmo depende de la cantidad de tiempo, almacenamiento y otros recursos necesarios para ejecutar el algoritmo. La eficiencia se mide con la ayuda de notaciones asintóticas.
Un algoritmo puede no tener el mismo rendimiento para diferentes tipos de entradas. Con el aumento del tamaño de la entrada, el rendimiento cambiará.
El estudio del cambio en el rendimiento del algoritmo con el cambio en el orden del tamaño de la entrada se define como análisis asintótico.
Notaciones asintóticas
Las notaciones asintóticas son las notaciones matemáticas utilizadas para describir el tiempo de ejecución de un algoritmo cuando la entrada tiende hacia un valor particular o un valor límite.
Por ejemplo: En la ordenación de burbujas, cuando el array de entrada ya está ordenado, el tiempo que tarda el algoritmo es lineal, es decir, el mejor caso.
Pero, cuando el array de entrada está en condición inversa, el algoritmo tarda el máximo tiempo (cuadrático) en ordenar los elementos, es decir, el peor caso.
Cuando el array de entrada no está ni ordenado ni en condición inversa, entonces tarda un tiempo medio. Estas duraciones se denotan utilizando notaciones asintóticas.
Hay principalmente tres notaciones asintóticas:
- Notación Big-O
- Notación Omega
- Notación Theta
Notación Big-O (anotación O)
La notación Big-O representa el límite superior del tiempo de ejecución de un algoritmo. Por lo tanto, da la complejidad en el peor caso de un algoritmo.
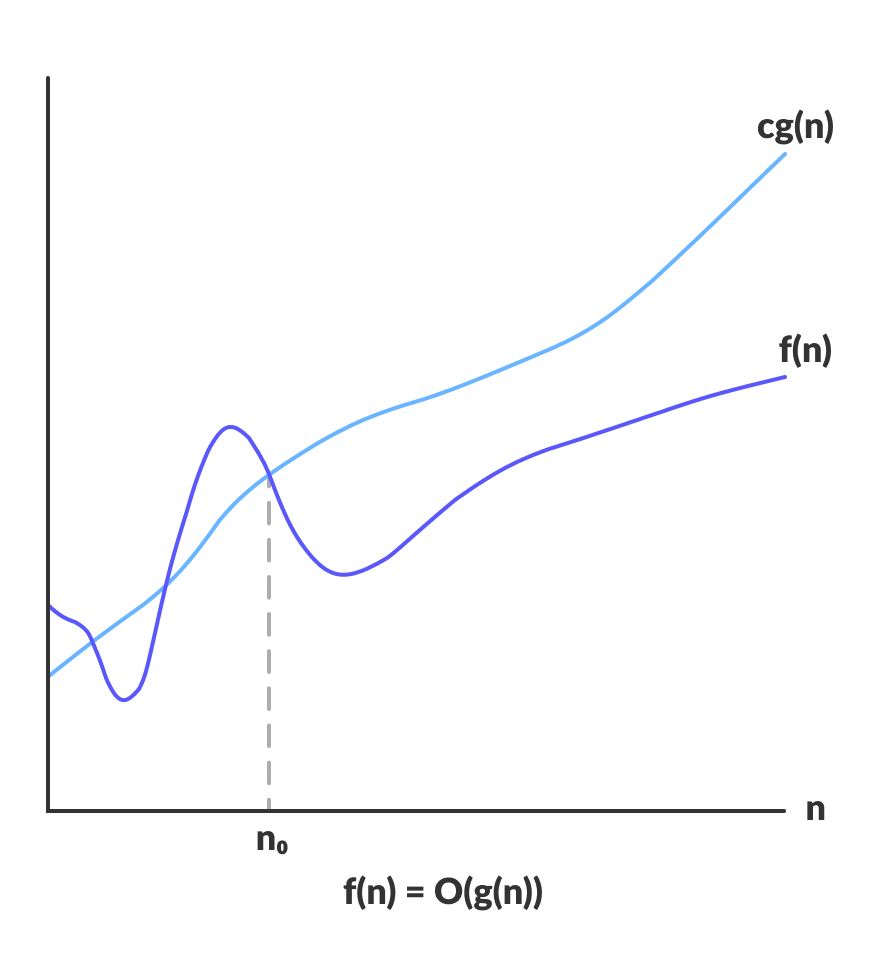
O(g(n)) = { f(n): there exist positive constants c and n0 such that 0 ≤ f(n) ≤ cg(n) for all n ≥ n0 }
La expresión anterior puede describirse como una función f(n) pertenece al conjunto O(g(n)) si existe una constante positiva c tal que se encuentra entre 0 y cg(n), para un n suficientemente grande.
n, el tiempo de ejecución de un algoritmo no cruza el tiempo proporcionado por O(g(n)).
Dado que proporciona el tiempo de ejecución del peor caso de un algoritmo, se utiliza ampliamente para analizar un algoritmo ya que siempre estamos interesados en el peor caso.
Notación Omega (Ω-notación)
La notación Omega representa el límite inferior del tiempo de ejecución de un algoritmo. Así, proporciona la complejidad del mejor caso de un algoritmo.

Ω(g(n)) = { f(n): there exist positive constants c and n0 such that 0 ≤ cg(n) ≤ f(n) for all n ≥ n0 }
La expresión anterior puede describirse como una función f(n) pertenece al conjunto Ω(g(n)) si existe una constante positiva c tal que está por encima de cg(n), para un n suficientemente grande.
Para cualquier valor de n, el tiempo mínimo requerido por el algoritmo viene dado por Omega Ω(g(n)).
Notación Theta (Θ-notación)
La notación Theta encierra la función por arriba y por abajo. Dado que representa el límite superior y el inferior del tiempo de ejecución de un algoritmo, se utiliza para analizar la complejidad del caso medio de un algoritmo.
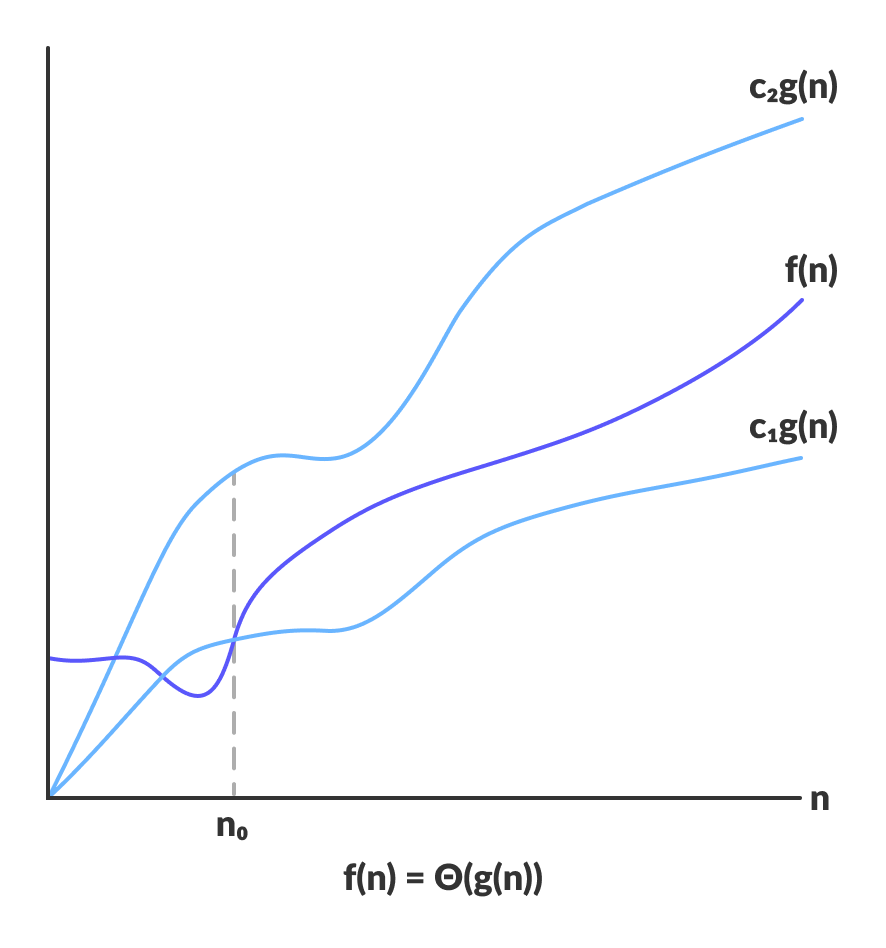
Para una función g(n)Θ(g(n)) viene dada por la relación:
Θ(g(n)) = { f(n): there exist positive constants c1, c2 and n0 such that 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n) for all n ≥ n0 }
La expresión anterior puede describirse como una función f(n) pertenece al conjunto Θ(g(n)) si existen constantes positivas c1 y c2 tales que se puede intercalar entre c1g(n) y c2g(n), para un n suficientemente grande.
Si una función f(n) se encuentra en cualquier lugar entre c1g(n) y c2g(n) para todo n ≥ n0, entonces f(n) se dice que está acotado asintóticamente.