
Seré sincero. Llevo más años de los que me gustaría admitir haciendo cosas serias de cálculo. A veces, en física, simplemente hay que integrar cosas. Es lo que pasa.
Sin embargo, cuando estaba ayudando a mi hijo con su clase de cálculo empecé a darme cuenta -¿qué demonios pasa con la integración? Siento que tengo una comprensión muy sólida de las derivadas – pero la integración tiene algunas cosas raras.
Bueno, nunca vas a entender las cosas hasta que las descompongas en sus piezas básicas. Así que eso es lo que voy a hacer. Voy a encontrar el área bajo una curva de tres maneras diferentes.
Área usando la notación de suma
Esta es la más fácil de entender, pero la más difícil de calcular. ¡Oh, espera! Por qué estamos encontrando el área bajo una curva? Bien, espera – mi ejemplo al final debería ayudar.
Así que la idea básica es dividir un área en N rectángulos (donde N es sólo un número). Entonces puedo encontrar el área de cada rectángulo y sumarlos para obtener el área total. Cuantos más trozos divida, mejor será la respuesta, así que escribiré una expresión para esta área y tomaré el límite a medida que el número de trozos llegue al infinito.

El área se calcularía entonces como:
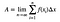
Hay muchas cosas después de esto – y se vuelve un poco tedioso. Sin embargo, usted DEBE ir a través de esto para entender completamente la cosa. Aquí hay un video en el que te guío a través de él.
Si usas una función:
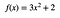
El área desde x = 1 hasta x =2 es 9 (cualquiera que sean las unidades – no soy matemático, así que me molesta omitir las unidades).
Área usando antiderivadas
Hay un truco. Es un truco impresionante. Puedes escribir el área bajo una curva como una integral definida (donde la integral es una suma infinita de trozos infinitamente pequeños – igual que la notación de la suma).
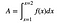
Ahora la locura. LOCURA. Resulta que el área es la antiderivada de f(x). Si te paras un momento, verás que eso es salvaje. Una locura salvaje. Si la derivada te dice algo sobre la pendiente de una curva, la antiderivada te dice sobre el área bajo la curva…
Sí. Es el teorema fundamental del cálculo. Aquí está mi explicación (sí, va a haber un montón de vídeos en este post y estás OBLIGADO a verlos todos.
En realidad, aquí hay otra cosa importante. La integral definida de x = 1 a x =2 es la diferencia de la función área A(2) y A(1). No voy a repasar los detalles de eso porque todavía tengo la mente en blanco con lo de la antiderivada.
Pero aquí está el área bajo la MISMA función pero con integración.
Sí. Se obtiene el mismo resultado final. Área = 9 pollos² (he añadido las unidades de área).
Área mediante cálculos numéricos
Ahora llegamos a lo divertido. Qué pasa si encuentro el área bajo una curva sumando el área de un montón de rectángulos? Oh, espera… eso ya lo hice en el primer método. ¿Pero qué tal esto – no hago un número infinito de rectángulos, sólo hago un gran número de rectángulos? Eso es exactamente lo que es un cálculo numérico.
Por supuesto, si rompo un área en 100 piezas voy a tener que hacer 100 conjuntos de cálculos de área. Realmente alguien quiere hacer eso? No – nadie piensa que eso sería divertido. ¿Pero sabes a quién no le importa? Los ordenadores (ordenadores electrónicos).
Sí, podemos conseguir que un ordenador haga esta serie de cálculos. Sólo tenemos que darle unas instrucciones y luego irá a hacer su trabajo. Será genial. Esta es la receta básica que utilizará.
- Decide en cuántos trozos quieres dividir la curva. ¿Qué tal 100? Con esto y el valor x inicial y final, puedes calcular el ancho de cada rectángulo (Δx).
- Pon el área a cero (pollos²). Vamos a seguir añadiendo a este valor, pero tiene que empezar en alguna parte.
- Empezar con el valor x inicial (en el ejemplo que he estado usando – que es x = 1).
- Calcular la altura del rectángulo. Esto sería f(x) en el valor actual de x.
- Encuentra el área de este rectángulo y súmala al área total.
- Muévete en el siguiente valor de x y repite hasta llegar a la x final.
Es tan sencillo que hasta un ordenador podría hacerlo. Vale, sólo me estoy divirtiendo. Algunos de mis mejores amigos son los ordenadores.
Aquí está el código para este cálculo en python (aquí hay un enlace al código real).
def f(t):
return(3*t**2+2)N=100x1=1
x2=2dx=(x2-x1)/N
A=0
x=x1
while x<=x2:
dA=f(x)*dx
A=A+dA
x=x+dx
print("A = ",A)
Con N = 100, obtengo un área de 8,95505 – que NO es exactamente 9 pollos², pero se acerca bastante. Lo suficientemente cerca para la mayoría de los cálculos de pollos cuadrados.
Sólo unos pocos comentarios rápidos sobre este código.
- Pensé que sería divertido hacer la función una función real de python (esa es la parte
def f(t):. - Primero calculo el área del rectángulo diminuto (dA) y luego lo sumo al área total.
- Este método en realidad tiene rectángulos alineados con la función en el lado izquierdo de la parte superior del rectángulo. Usted podría hacerlo con el lado derecho también.
- También hice un video para esto. Pero no es necesario que lo veas – en su mayor parte ya lo expliqué aquí.
¿Y si no tienes una función matemática?
Déjame ponerte en la siguiente situación. Estás en un coche que circula y sólo puedes ver el velocímetro. Anotas el valor de la velocidad cada segundo (porque eres súper rápido tomando notas). Al final el coche se para y necesitas averiguar cuánto has viajado.
Aquí tienes algo parecido (usando un carro Vernier con un sensor de movimiento – pero te haces a la idea de que esto es lo mismo que un coche real).

OK – aviso, Voy a hacer trampa aquí. La pista Vernier recoge datos de posición basados en estas líneas de la pista. A partir de los datos de posición, calcula la velocidad. Por lo tanto, ya tengo la posición del carro – pero vamos a pretender que sólo da la velocidad en función del tiempo. Quizás quedaría algo así.

Ver. Eso no es una función – es una estación espacial. No, espera – eso es de Star Wars. Pero aún así, no es una función matemática. Son sólo datos. No puedes encontrar la antiderivada de los datos (bueno, no usando las reglas normales y demás). Pero ¡espera! La integración numérica funciona bien.
Por supuesto, hay algo más importante aquí. Es la idea de que el área bajo esta curva representa algo real. Imagina que tienes un coche moviéndose con una velocidad constante durante algún tiempo. Podrías calcular el desplazamiento con bastante facilidad:
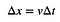
Si tienes un gráfico de velocidad vs. tiempo, esta velocidad constante se vería como un rectángulo. Sí, el área de ese rectángulo sería v*Δt. Si NO es una velocidad constante, el área bajo la gráfica velocidad-tiempo seguiría siendo el desplazamiento.
Ok, un último vídeo. Aquí está mi explicación de la codificación para resolver este problema de desplazamiento.
Asegúrate de ver todos los vídeos.