Deterministische endliche Automaten
Ein deterministischer endlicher Automat (DFA) wird durch ein fünfgliedriges Tupel beschrieben: (Q,Σ,δ,q0,F)(Q, \Sigma, \delta, q_0, F)(Q,Σ,δ,q0,F).
QQQQ = eine endliche Menge von Zuständen
Σ\SigmaΣ = ein endliches, nichtleeres Eingabealphabet
δ\deltaδ = eine Reihe von Übergangsfunktionen
q0q_0q0 = der Anfangszustand
FFF = die Menge der akzeptierenden Zustände
Es muss genau eine Übergangsfunktion für jedes Eingabesymbol in Σ\SigmaΣ aus jedem Zustand geben.
DFAs können durch Diagramme dieser Form dargestellt werden: 
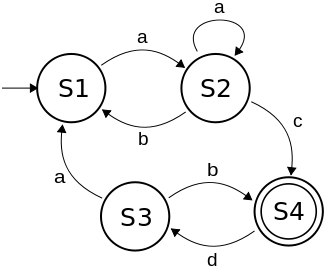
Welche Zeichenkette kann von dem folgenden endlichen Zustandsautomaten nicht erzeugt werden?
Hier ist ein DFA-Diagramm, das ein paar einfache Bewegungen beschreibt, die eine Figur in einem Videospiel ausführen kann: stehen, laufen und springen. Die Tasten, mit denen ein Spieler diesen bestimmten Charakter steuern kann, sind „Auf“, „A“, oder der Spieler kann keine Taste drücken.

Beschreiben Sie anhand des Zustandsdiagramms für die Videospielfigur oben, wie ein Spieler seine Figur steuern kann, um vom Stehen über das Laufen zum Springen zu gelangen.
Antwort anzeigenIm stehenden Zustand kann der Spieler nichts drücken und im stehenden Zustand verbleiben, dann, um in den laufenden Zustand überzugehen, muss der Benutzer die Taste „Auf“ drücken. Im Laufzustand kann der Benutzer seinen Charakter weiterlaufen lassen, indem er die Taste „Nach oben“ drückt, und dann, um in den Sprungzustand überzugehen, muss der Benutzer „A“ drücken.
Zeichne ein Diagramm für einen DFA, der die folgende Sprache erkennt: Die Sprache aller Zeichenketten, die mit einer 1 enden.
Antwort anzeigen
Nichtdeterministische endliche Automaten
QQQQ = eine endliche Menge von Zuständen
Σ\SigmaΣ = ein endliches, nicht-leeres Eingabealphabet
δ\deltaδ = eine Reihe von Übergangsfunktionen
q0q_0q0 = der Anfangszustand
FFF = die Menge der akzeptierenden Zustände
Im Gegensatz zu DFAs müssen NDFAs nicht für jedes Symbol in Σ\SigmaΣ Übergangsfunktionen haben, und es kann mehrere Übergangsfunktionen im gleichen Zustand für das gleiche Symbol geben. Zusätzlich können NDFAs Null-Übergänge verwenden, die durch ϵ\epsilonϵ gekennzeichnet sind. Null-Übergänge erlauben es der Maschine, von einem Zustand in einen anderen zu springen, ohne ein Symbol lesen zu müssen.
Ein NDFA akzeptiert eine Zeichenkette xxx, wenn es einen Pfad gibt, der mit dieser Zeichenkette kompatibel ist und in einem akzeptierten Zustand endet.
NDFAs können durch Diagramme dieser Form dargestellt werden:
 Quelle
Quelle
Beschreiben Sie die Sprache, die die obige NDFA erkennt.
Antwort anzeigenDas obige NDFA erkennt Zeichenketten, die auf „10“ enden, und Zeichenketten, die auf „01“ enden.
Der Zustand aaa ist der Startzustand, und von dort aus können wir eine Zeichenkette mit beliebig vielen 1en und 0en in beliebiger Reihenfolge erzeugen und dann in den Zustand bbb oder eee übergehen, oder wir können sofort in den Zustand bbb oder eee übergehen. In jedem Fall akzeptiert der NDFA nur eine Zeichenkette, die den Zustand ddd oder den Zustand ggg erreicht. Um den Zustand ddd oder ggg zu erreichen, muss die Zeichenkette mit einer „01“ (für den Zustand ddd) oder einer „10“ (für den Zustand ggg) enden.
Beispielsweise werden die folgenden Zeichenketten alle von diesem NDFA erkannt.
- 00000000010
- 10
- 01
- 1111101
Welche Zeichenkette kann nicht durch den folgenden endlichen Automaten erzeugt werden?

Zeichnen Sie ein Diagramm für den NDFA, das die folgende Sprache beschreibt: Die Sprache aller Strings, die mit einer 1 enden.
Antwort anzeigen

