Einführende Chemie – 1. Kanadische Ausgabe

Gase gehörten zu den ersten Substanzen, die mit der modernen wissenschaftlichen Methode untersucht wurden, die in den 1600er Jahren entwickelt wurde. Es dauerte nicht lange, bis man erkannte, dass alle Gase bestimmte physikalische Verhaltensweisen gemeinsam hatten, was nahelegte, dass Gase durch eine allumfassende Theorie beschrieben werden könnten. Die kinetische Molekulartheorie der Gase ist ein Modell, das uns hilft, die physikalischen Eigenschaften von Gasen auf molekularer Ebene zu verstehen. Sie basiert auf den folgenden Konzepten:

1. Gase bestehen aus Teilchen (Molekülen oder Atomen), die sich in ständiger zufälliger Bewegung befinden.
2. Gasteilchen kollidieren ständig miteinander und mit den Wänden ihres Behälters. Diese Kollisionen sind elastisch, d.h. es gibt keinen Netto-Energieverlust durch die Kollisionen.
3. Gasteilchen sind klein und das Gesamtvolumen, das von Gasmolekülen eingenommen wird, ist vernachlässigbar im Verhältnis zum Gesamtvolumen ihres Behälters.
4. Es gibt keine interaktiven Kräfte (d.h., Anziehung oder Abstoßung) zwischen den Teilchen eines Gases.
5. Die durchschnittliche kinetische Energie der Gasteilchen ist proportional zur absoluten Temperatur des Gases, und alle Gase bei gleicher Temperatur haben die gleiche durchschnittliche kinetische Energie.

Abbildung 6.6 „Die kinetische Molekültheorie der Gase“ zeigt eine Darstellung, wie wir uns die Gasphase gedanklich vorstellen.

Die kinetische Molekültheorie der Gase beschreibt diesen Zustand der Materie als aus winzigen Teilchen in ständiger Bewegung mit viel Abstand zwischen den Teilchen bestehend. Da der größte Teil des von einem Gas eingenommenen Volumens leerer Raum ist, hat ein Gas eine geringe Dichte und kann sich unter entsprechendem Einfluss ausdehnen oder zusammenziehen. Die Tatsache, dass sich Gasteilchen in ständiger Bewegung befinden, bedeutet, dass sich zwei oder mehr Gase immer vermischen werden, da sich die Teilchen der einzelnen Gase bewegen und miteinander kollidieren. Die Anzahl der Zusammenstöße der Gasteilchen mit den Wänden ihres Behälters und die Kraft, mit der sie zusammenstoßen, bestimmen die Größe des Gasdrucks.

Kinetische Energie und Molekulargeschwindigkeit

Gasteilchen sind in ständiger Bewegung, und jedes Objekt in Bewegung hat kinetische Energie (Ek). Die kinetische Energie kann für ein einzelnes Atom mit der folgenden Gleichung berechnet werden, wobei m die Masse und u die Geschwindigkeit ist.

Ek = 1/2 mu2

Gesamt haben die Moleküle in einer Gasprobe eine durchschnittliche kinetische Energie; einzelne Moleküle weisen jedoch eine Verteilung der kinetischen Energie auf, weil sie eine Verteilung der Geschwindigkeiten haben (Abbildung 6.7 „Stilisierte Molekulargeschwindigkeitsverteilung“). Diese Geschwindigkeitsverteilung ergibt sich aus den Stößen, die zwischen den Molekülen in der Gasphase stattfinden. Obwohl diese Zusammenstöße elastisch sind (es gibt keinen Netto-Energieverlust), können sich die individuellen Geschwindigkeiten der einzelnen an der Kollision beteiligten Moleküle ändern. Zum Beispiel kann bei der Kollision zweier Moleküle ein Molekül mit einer etwas höheren Geschwindigkeit und das andere mit einer etwas niedrigeren Geschwindigkeit abgelenkt werden, aber die durchschnittliche kinetische Energie ändert sich nicht.

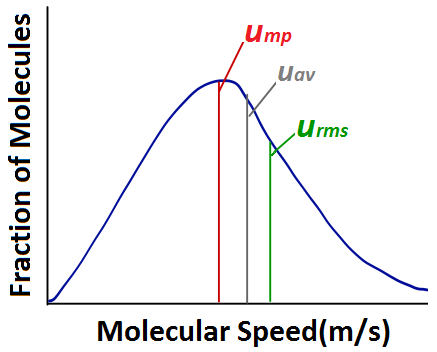
Bei der Analyse eines Diagramms der Verteilung der molekularen Geschwindigkeiten gibt es einige gebräuchliche Begriffe, mit denen man vertraut sein sollte. Die wahrscheinlichste Geschwindigkeit (ump) ist die Geschwindigkeit der größten Anzahl von Molekülen und entspricht der Spitze der Verteilung. Die Durchschnittsgeschwindigkeit (uav) ist die mittlere Geschwindigkeit aller Gasmoleküle in der Probe. Die Effektivgeschwindigkeit (urms) entspricht der Geschwindigkeit von Molekülen, die genau die gleiche kinetische Energie haben wie die durchschnittliche kinetische Energie der Probe.

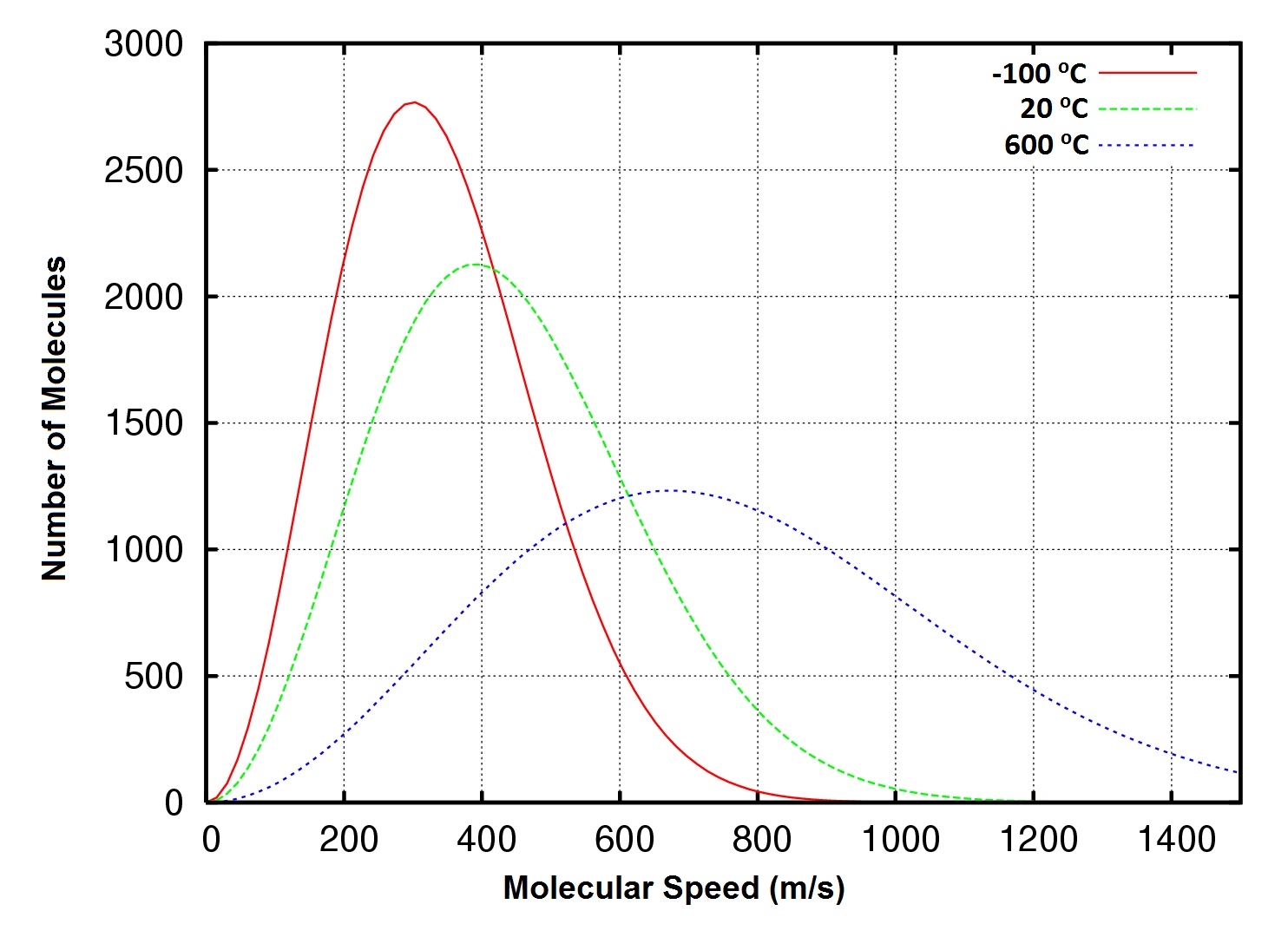
Abbildung 6.8 Verteilung der molekularen Geschwindigkeiten, Sauerstoffgas bei -100, 20 und 600°C

Nach der kinetischen Molekültheorie ist die mittlere kinetische Energie der Gasteilchen proportional zur absoluten Temperatur des Gases. Dies kann mit der folgenden Gleichung ausgedrückt werden, wobei k die Boltzmann-Konstante darstellt. Die Boltzmann-Konstante ist einfach die Gaskonstante R geteilt durch die Avogadro-Konstante (NA). Der Balken über bestimmten Termen zeigt an, dass es sich um Durchschnittswerte handelt.

\overline{E_k} = \frac{3}{2} \textit{kT}

Da die mittlere kinetische Energie sowohl mit der absoluten Temperatur als auch mit der Molekulargeschwindigkeit zusammenhängt, können wir die obige Gleichung mit der vorherigen kombinieren, um die Effektivgeschwindigkeit zu bestimmen.

\overline{E_k} \textit{ = }\frac{1}{2} \textit{m} \overline{u^2} \textit{ = } \frac{3}{2} \textit{kT}

$\sqrt{\overline{u^2}} = \sqrt{\frac{3kT}{m}$

Dies zeigt, dass die Effektivgeschwindigkeit mit der Temperatur zusammenhängt. Wir können diese Gleichung weiter manipulieren, indem wir den Zähler und den Nenner mit der Avogadro-Konstante (NA) multiplizieren, um eine Form zu erhalten, die die Gaskonstante (R) und die molare Masse (M) verwendet.

$$sqrt{\overline{u^2}}\ = \sqrt{\frac{3RT}{M}}$

Diese Form der Gleichung zeigt, dass die Effektivgeschwindigkeit von Gasmolekülen auch mit der molaren Masse der Substanz zusammenhängt. Vergleicht man zwei Gase mit unterschiedlicher Molmasse bei gleicher Temperatur, so sieht man, dass trotz gleicher mittlerer kinetischer Energie das Gas mit der kleineren Molmasse eine höhere Effektivgeschwindigkeit hat.

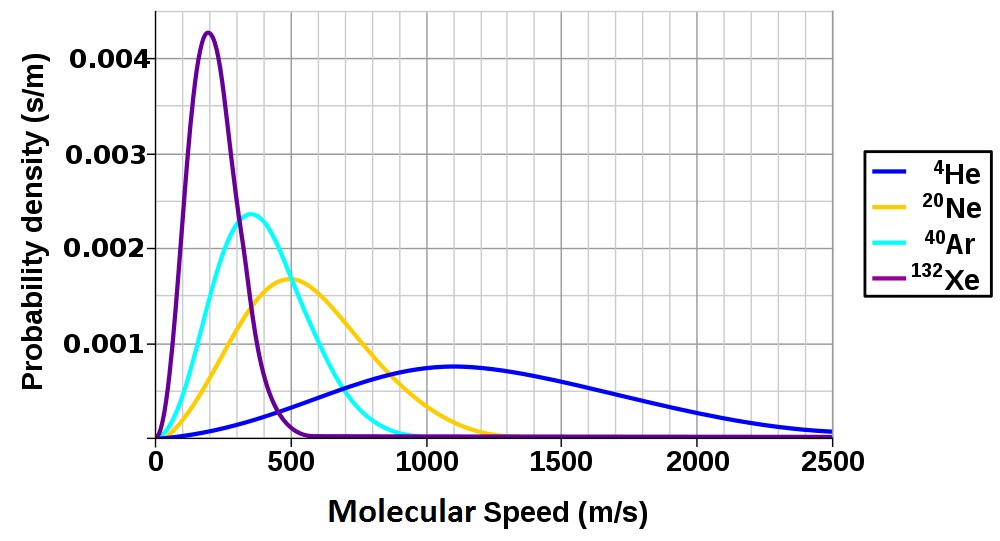
Abbildung 6.9 Molekulargeschwindigkeitsverteilung edler Gase

Anwendung der kinetischen Molekulartheorie auf die Gasgesetze

Die kinetische Molekulartheorie kann verwendet werden, um die experimentellen Trends zu erklären oder vorherzusagen, die zur Erstellung der Gasgesetze verwendet wurden. Lassen Sie uns ein paar Szenarien durcharbeiten, um diesen Punkt zu demonstrieren.

Was passiert mit dem Druck eines Systems, bei dem das Volumen bei konstanter Temperatur verringert wird?

Dieses Problem kann auf zwei Arten angegangen werden:

1. Das ideale Gasgesetz kann umgeordnet werden, um für den Druck zu lösen und die Druckänderung abzuschätzen:

Textit{PV = nRT}

Textit{P = }\frac{nRT}{V}\textit{}

Das Volumen steht im Nenner der Gleichung, und es wird verringert. Das bedeutet, dass der Rest der Gleichung durch eine kleinere Zahl geteilt wird, so dass der Druck größer werden sollte.

2. Die kinetische Molekulartheorie kann verwendet werden. Da die Temperatur konstant bleibt, bleiben auch die mittlere kinetische Energie und die Effektivgeschwindigkeit gleich. Das Volumen des Behälters hat sich verringert, was bedeutet, dass die Gasmoleküle eine kürzere Strecke zurücklegen müssen, um eine Kollision zu haben. Es gibt also mehr Zusammenstöße pro Sekunde, was zu einem Druckanstieg führt.

Was passiert mit dem Druck eines Systems, bei dem die Temperatur erhöht wird und das Volumen konstant bleibt?

Auch diese Art von Problem kann auf zwei Arten angegangen werden:

1. Das ideale Gasgesetz kann umgeordnet werden, um für den Druck zu lösen und die Druckänderung abzuschätzen.

Textit{p = }\frac{nRT}{V}\textit{}

Die Temperatur steht im Zähler; es besteht ein direkter Zusammenhang zwischen Temperatur und Druck. Daher sollte eine Erhöhung der Temperatur eine Erhöhung des Drucks bewirken.

2. Die kinetische Molekulartheorie kann verwendet werden. Die Temperatur wird erhöht, also sollten auch die mittlere kinetische Energie und die Effektivgeschwindigkeit steigen. Das bedeutet, dass die Gasmoleküle häufiger und mit größerer Kraft auf die Behälterwände treffen werden, weil sie sich alle schneller bewegen. Dadurch sollte sich der Druck erhöhen.