Die Notwendigkeit, zwischen den verschiedenen Bedeutungen von „Bezugsrahmen“ zu unterscheiden, hat zu einer Vielzahl von Begriffen geführt. Zum Beispiel wird manchmal die Art des Koordinatensystems als Modifikator angehängt, wie in kartesischem Bezugssystem. Manchmal wird der Zustand der Bewegung betont, wie in rotierendem Bezugssystem. Manchmal wird die Art und Weise der Transformation zu als zusammengehörig betrachteten Rahmen hervorgehoben, wie in Galilei-Bezugsrahmen. Manchmal werden Rahmen durch den Maßstab ihrer Beobachtungen unterschieden, wie bei makroskopischen und mikroskopischen Bezugsrahmen.
In diesem Artikel wird der Begriff Beobachtungsrahmen verwendet, wenn die Betonung auf dem Bewegungszustand liegt und nicht auf der Koordinatenwahl oder dem Charakter der Beobachtungen oder des Beobachtungsapparats. In diesem Sinne erlaubt ein Beobachtungs-Bezugsrahmen die Untersuchung der Wirkung von Bewegung auf eine ganze Familie von Koordinatensystemen, die an diesen Rahmen angehängt werden können. Andererseits kann ein Koordinatensystem für viele Zwecke verwendet werden, bei denen der Zustand der Bewegung nicht das primäre Anliegen ist. Zum Beispiel kann ein Koordinatensystem verwendet werden, um die Symmetrie eines Systems auszunutzen. In einer noch breiteren Perspektive verwendet die Formulierung vieler Probleme in der Physik verallgemeinerte Koordinaten, Normalmoden oder Eigenvektoren, die nur indirekt mit Raum und Zeit zu tun haben. Für die folgende Diskussion erscheint es sinnvoll, die verschiedenen Aspekte eines Bezugsrahmens zu trennen. Wir betrachten daher Beobachtungsrahmen, Koordinatensysteme und Beobachtungsgeräte als unabhängige Konzepte, die wie folgt getrennt werden:
- Ein Beobachtungsrahmen (wie z.B. ein Inertialrahmen oder ein nicht-inertialer Bezugsrahmen) ist ein physikalisches Konzept, das sich auf den Bewegungszustand bezieht.
- Ein Koordinatensystem ist ein mathematisches Konzept, das auf eine Wahl der Sprache hinausläuft, die zur Beschreibung von Beobachtungen verwendet wird. Folglich kann ein Beobachter in einem Bezugsrahmen ein beliebiges Koordinatensystem (kartesisch, polar, krummlinig, verallgemeinert, …) wählen, um Beobachtungen zu beschreiben, die von diesem Bezugsrahmen aus gemacht werden. Eine Änderung in der Wahl dieses Koordinatensystems ändert nicht den Bewegungszustand eines Beobachters und hat somit auch keine Änderung des Beobachtungsrahmens des Beobachters zur Folge. Diese Sichtweise findet sich auch an anderer Stelle wieder. Damit soll nicht bestritten werden, dass manche Koordinatensysteme für manche Beobachtungen besser geeignet sind als andere.
- Die Entscheidung, was gemessen werden soll und mit welchem Beobachtungsapparat, ist eine Angelegenheit, die vom Bewegungszustand des Beobachters und der Wahl des Koordinatensystems unabhängig ist.
Hier ist ein Zitat, das auf bewegte Beobachtungsrahmen R

und verschiedene zugehörige euklidische Drei-Raum-Koordinatensysteme :
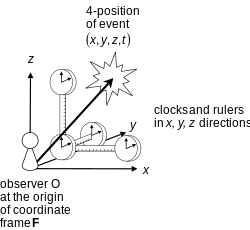
Wir führen zunächst den Begriff des Bezugsrahmens ein, der seinerseits mit der Idee des Beobachters zusammenhängt: Der Bezugsrahmen ist in gewissem Sinne der „euklidische Raum, den der Beobachter trägt“. Lassen Sie uns eine mathematischere Definition geben: … der Bezugsrahmen ist … die Menge aller Punkte im euklidischen Raum mit der Starrkörperbewegung des Beobachters. Der Rahmen, bezeichnet mit R…
, soll sich mit dem Beobachter bewegen…. Die räumlichen Positionen der Teilchen werden relativ zu einem Rahmen R {\displaystyle {\mathfrak {R}} bezeichnet}
bezeichnet, indem man ein Koordinatensystem R mit Ursprung O aufstellt. Der entsprechende Satz von Achsen, die die Starrkörperbewegung des Rahmens R {\displaystyle {\mathfrak {R}}
, kann als eine physikalische Realisierung von R {\displaystyle {\mathfrak {R}}
. In einem Rahmen R {\displaystyle {\mathfrak {R}}
, werden die Koordinaten von R nach R′ verändert, indem zu jedem Zeitpunkt dieselbe Koordinatentransformation an den Komponenten der Eigenobjekte (Vektoren und Tensoren) durchgeführt wird, die zur Darstellung physikalischer Größen in diesem Rahmen eingeführt wurden.
Und dies über den Nutzen der Trennung der Begriffe von R

und :
Wie von Brillouin bemerkt, muss eine Unterscheidung zwischen mathematischen Koordinatensätzen und physikalischen Bezugsrahmen getroffen werden. Die Unkenntnis dieser Unterscheidung ist die Quelle vieler Verwirrungen… die abhängigen Funktionen, wie z.B. die Geschwindigkeit, werden in Bezug auf einen physikalischen Bezugsrahmen gemessen, aber man ist frei, jedes beliebige mathematische Koordinatensystem zu wählen, in dem die Gleichungen angegeben sind.
und dies, auch zur Unterscheidung zwischen R {\displaystyle {\mathfrak {R}}

und :
Die Idee eines Bezugsrahmens ist eigentlich eine ganz andere als die eines Koordinatensystems. Rahmen unterscheiden sich nur dann, wenn sie unterschiedliche Räume (Mengen von Ruhepunkten) oder Zeiten (Mengen von gleichzeitigen Ereignissen) definieren. Die Vorstellungen von einem Raum, einer Zeit, von Ruhe und Gleichzeitigkeit sind also untrennbar mit dem Begriff des Rahmens verbunden. Eine bloße Verschiebung des Ursprungs oder eine rein räumliche Drehung der Raumkoordinaten führt jedoch zu einem neuen Koordinatensystem. Rahmen entsprechen also bestenfalls Klassen von Koordinatensystemen.
und von J. D. Norton:
In den traditionellen Entwicklungen der Speziellen und Allgemeinen Relativitätstheorie war es üblich, nicht zwischen zwei ganz unterschiedlichen Ideen zu unterscheiden. Die erste ist der Begriff des Koordinatensystems, der einfach als die glatte, invertierbare Zuordnung von vier Zahlen zu Ereignissen in der Raumzeit-Nachbarschaft verstanden wird. Das zweite, das Bezugssystem, bezieht sich auf ein idealisiertes System, das verwendet wird, um solche Zahlen zuzuordnen. Um unnötige Einschränkungen zu vermeiden, können wir diese Anordnung von metrischen Begriffen trennen. Von besonderer Bedeutung für unsere Zwecke ist, dass jedes Bezugssystem bei jedem Ereignis der Raumzeit einen bestimmten Bewegungszustand hat. Im Rahmen der Speziellen Relativitätstheorie und solange wir uns auf Bezugssysteme in Inertialbewegung beschränken, hängt wenig von der Differenz zwischen einem Inertialbezugssystem und dem von ihm induzierten Inertialkoordinatensystem ab. Dieser bequeme Umstand hört sofort auf, sobald wir beginnen, Bezugsrahmen in ungleichförmiger Bewegung zu betrachten, sogar innerhalb der Speziellen Relativitätstheorie…..In jüngerer Zeit ist der Begriff des Bezugsrahmens als eine von einem Koordinatensystem verschiedene Struktur wieder aufgetaucht, um die offensichtlichen Zweideutigkeiten von Einsteins Behandlung zu verhandeln.
Die Diskussion wird von Brading und Castellani über einfache Raum-Zeit-Koordinatensysteme hinausgeführt. Die Erweiterung auf Koordinatensysteme mit verallgemeinerten Koordinaten liegt den Hamilton- und Lagrangeschen Formulierungen der Quantenfeldtheorie, der klassischen relativistischen Mechanik und der Quantengravitation zugrunde.
KoordinatensystemeBearbeiten
Obwohl der Begriff „Koordinatensystem“ oft (vor allem von Physikern) in einem nicht-technischen Sinne verwendet wird, hat der Begriff „Koordinatensystem“ in der Mathematik eine genaue Bedeutung, und manchmal ist es das, was der Physiker auch meint.
Ein Koordinatensystem ist in der Mathematik eine Facette der Geometrie oder der Algebra, insbesondere eine Eigenschaft von Mannigfaltigkeiten (z. B. in der Physik, Konfigurationsräume oder Phasenräume). Die Koordinaten eines Punktes r in einem n-dimensionalen Raum sind einfach eine geordnete Menge von n Zahlen:
r = .

In einem allgemeinen Banach-Raum könnten diese Zahlen (zum Beispiel) Koeffizienten in einer funktionalen Erweiterung wie einer Fourier-Reihe sein. In einem physikalischen Problem könnten sie Raumzeitkoordinaten oder Normalmodenamplituden sein. In einem Roboterdesign könnten sie Winkel von relativen Rotationen, lineare Verschiebungen oder Verformungen von Gelenken sein. Hier nehmen wir an, dass diese Koordinaten durch einen Satz von Funktionen auf ein kartesisches Koordinatensystem bezogen werden können:
x j = x j ( x , y , z , … ) , j = 1 , … , n , {\displaystyle x^{j}=x^{j}(x,\ y,\ z,\ Punkte ),\quad j=1,\ Punkte ,\ n,}

wobei x, y, z, etc. die n kartesischen Koordinaten des Punktes sind. Angesichts dieser Funktionen sind Koordinatenflächen durch die Beziehungen definiert:
x j ( x , y , z , … ) = c o n s t a n t , j = 1 , … , n . {\displaystyle x^{j}(x,y,z,\dots )=\mathrm {konstant} ,\quad j=1,\dots ,\ n.}

Die Schnittpunkte dieser Flächen definieren Koordinatenlinien. An jedem ausgewählten Punkt definieren die Tangenten an die sich schneidenden Koordinatengeraden in diesem Punkt eine Menge von Basisvektoren {e1, e2, …, en} in diesem Punkt. Das ist:
e i ( r ) = lim ϵ → 0 r ( x 1 , … , x i + ϵ , … , x n ) – r ( x 1 , … , x i , … , x n ) ϵ , i = 1 , … , n , {\displaystyle \mathbf {e} _{i}(\mathbf {r} )=\lim _{\epsilon \rightarrow 0}{\frac {\mathbf {r} \left(x^{1},\ \dots ,\ x^{i}+\epsilon ,\ \ \dots ,\ x^{n}\right)-\mathbf {r} \left(x^{1},\ \dots ,\ x^{i},\ \dots ,\ x^{n}\right)}{\epsilon }},\quad i=1,\ \dots ,\ n,}

die auf Einheitslänge normiert werden kann. Näheres siehe Krummlinige Koordinaten.
Koordinatenflächen, Koordinatenlinien und Basisvektoren sind Bestandteile eines Koordinatensystems. Wenn die Basisvektoren in jedem Punkt orthogonal sind, ist das Koordinatensystem ein orthogonales Koordinatensystem.
Ein wichtiger Aspekt eines Koordinatensystems ist sein metrischer Tensor gik, der die Bogenlänge ds im Koordinatensystem in Abhängigkeit von den Koordinaten bestimmt:
( d s ) 2 = g i k d x i d x k , {\displaystyle (ds)^{2}=g_{ik}\ dx^{i}\ dx^{k},}

wobei über wiederholte Indizes summiert wird.
Wie aus diesen Ausführungen ersichtlich ist, ist ein Koordinatensystem ein mathematisches Konstrukt, Teil eines axiomatischen Systems. Es gibt keine notwendige Verbindung zwischen Koordinatensystemen und physikalischer Bewegung (oder irgendeinem anderen Aspekt der Realität). Allerdings können Koordinatensysteme die Zeit als Koordinate enthalten und zur Beschreibung von Bewegung verwendet werden. So können Lorentz-Transformationen und Galilei-Transformationen als Koordinatentransformationen betrachtet werden.
Allgemeine und spezielle Themen von Koordinatensystemen können über die untenstehenden Siehe auch-Links verfolgt werden.
Beobachtete BezugssystemeBearbeiten

Ein Beobachtungsbezugssystem, oft auch als physikalisches Bezugssystem, Bezugsrahmen oder einfach als Rahmen bezeichnet, ist ein physikalisches Konzept, das sich auf einen Beobachter und dessen Bewegungszustand bezieht. Wir schließen uns hier der von Kumar und Barve vertretenen Auffassung an: Ein Beobachtungsrahmen ist nur durch seinen Bewegungszustand charakterisiert. In diesem Punkt herrscht jedoch keine Einigkeit. In der Speziellen Relativitätstheorie wird manchmal die Unterscheidung zwischen einem Beobachter und einem Rahmen gemacht. Nach dieser Auffassung ist ein Rahmen ein Beobachter plus ein Koordinatengitter, das als orthonormale rechtshändige Menge von raumartigen Vektoren senkrecht zu einem zeitartigen Vektor konstruiert ist. Siehe Doran. Diese eingeschränkte Sichtweise wird hier nicht verwendet und wird auch in Diskussionen über die Relativitätstheorie nicht allgemein angenommen. In der allgemeinen Relativitätstheorie ist die Verwendung allgemeiner Koordinatensysteme üblich (siehe z. B. die Schwarzschild-Lösung für das Gravitationsfeld außerhalb einer isolierten Kugel).
Es gibt zwei Arten von Beobachtungsbezugssystemen: inertiale und nicht-inertiale. Ein inertiales Bezugssystem ist definiert als eines, in dem alle Gesetze der Physik in ihrer einfachsten Form gelten. In der Speziellen Relativitätstheorie sind diese Rahmen durch Lorentz-Transformationen verbunden, die durch die Geschwindigkeit parametrisiert sind. In der Newton’schen Mechanik genügt es, dass das erste Newton’sche Gesetz gilt, d.h. ein Newton’sches Inertialsystem ist ein System, in dem sich ein freies Teilchen mit konstanter Geschwindigkeit auf einer Geraden bewegt oder in Ruhe ist. Diese Rahmen sind durch Galilei-Transformationen miteinander verbunden. Diese relativistischen und Newtonschen Transformationen werden in Räumen allgemeiner Dimension durch Darstellungen der Poincaré-Gruppe und der Galilei-Gruppe ausgedrückt.
Im Gegensatz zum Inertialsystem ist ein nicht-inertiales Bezugssystem eines, in dem fiktive Kräfte zur Erklärung von Beobachtungen herangezogen werden müssen. Ein Beispiel ist ein beobachtender Bezugsrahmen, der auf einen Punkt der Erdoberfläche zentriert ist. Dieses Bezugssystem kreist um den Erdmittelpunkt, wodurch fiktive Kräfte wie die Corioliskraft, die Zentrifugalkraft und die Gravitationskraft eingeführt werden. (Alle diese Kräfte, einschließlich der Schwerkraft, verschwinden in einem echten Inertial-Bezugsrahmen, der einer des freien Falls ist.)
MessapparatBearbeiten
Ein weiterer Aspekt eines Bezugsrahmens ist die Rolle des Messapparats (z. B. Uhren und Stäbe), der am Rahmen befestigt ist (siehe Norton-Zitat oben). Diese Frage wird in diesem Artikel nicht behandelt und ist vor allem in der Quantenmechanik von Interesse, wo die Beziehung zwischen Beobachter und Messung noch diskutiert wird (siehe Messproblem).
In physikalischen Experimenten wird der Bezugsrahmen, in dem die Messgeräte im Labor ruhen, meist als Laborrahmen oder einfach „Laborrahmen“ bezeichnet. Ein Beispiel wäre der Rahmen, in dem die Detektoren eines Teilchenbeschleunigers ruhen. In einigen Experimenten ist der Laborrahmen ein Inertialrahmen, aber er muss es nicht sein (zum Beispiel ist das Labor auf der Erdoberfläche in vielen physikalischen Experimenten nicht inertial). In Experimenten der Teilchenphysik ist es oft nützlich, Energien und Impulse von Teilchen aus dem Laborrahmen, in dem sie gemessen werden, in den Schwerpunktrahmen „COM-Frame“ zu transformieren, was die Berechnungen manchmal vereinfacht, da möglicherweise die gesamte kinetische Energie, die im COM-Frame noch vorhanden ist, für die Erzeugung neuer Teilchen verwendet werden kann.
In diesem Zusammenhang sei angemerkt, dass die Uhren und Stäbe, mit denen die Messgeräte der Beobachter in Gedanken oft beschrieben werden, in der Praxis durch eine viel kompliziertere und indirekte Metrologie ersetzt werden, die mit der Natur des Vakuums zusammenhängt und Atomuhren verwendet, die nach dem Standardmodell arbeiten und um die gravitative Zeitdilatation korrigiert werden müssen. (Siehe Sekunde, Meter und Kilogramm).
In der Tat war Einstein der Meinung, dass Uhren und Stäbe lediglich zweckmäßige Messgeräte sind und sie durch fundamentalere Einheiten ersetzt werden sollten, die zum Beispiel auf Atomen und Molekülen basieren.