Die Effizienz eines Algorithmus hängt davon ab, wie viel Zeit, Speicherplatz und andere Ressourcen zur Ausführung des Algorithmus benötigt werden. Die Effizienz wird mit Hilfe von asymptotischen Notationen gemessen.
Ein Algorithmus kann für verschiedene Arten von Eingaben nicht die gleiche Leistung haben. Mit der Zunahme der Eingabegröße ändert sich die Leistung.
Die Untersuchung der Änderung der Leistung des Algorithmus mit der Änderung der Reihenfolge der Eingabegröße wird als asymptotische Analyse definiert.
Asymptotische Notationen
Asymptotische Notationen sind die mathematischen Notationen, die verwendet werden, um die Laufzeit eines Algorithmus zu beschreiben, wenn die Eingabe zu einem bestimmten Wert oder einem Grenzwert tendiert.
Beispielsweise: Bei der Bubble-Sortierung ist die Zeit, die der Algorithmus benötigt, wenn das Eingabe-Array bereits sortiert ist, linear, d. h. der beste Fall.
Wenn sich das Eingabe-Array jedoch im umgekehrten Zustand befindet, benötigt der Algorithmus die maximale Zeit (quadratisch), um die Elemente zu sortieren, d. h. der schlechteste Fall.
Wenn das Eingabe-Array weder sortiert noch im umgekehrten Zustand ist, benötigt der Algorithmus durchschnittliche Zeit. Diese Zeiten werden mit asymptotischen Notationen angegeben.
Es gibt hauptsächlich drei asymptotische Notationen:
- Big-O-Notation
- Omega-Notation
- Theta-Notation
Big-O-Notation (O-Notation)
Die Big-O-Notation stellt die obere Grenze der Laufzeit eines Algorithmus dar. Sie gibt also die worst-case Komplexität eines Algorithmus an.
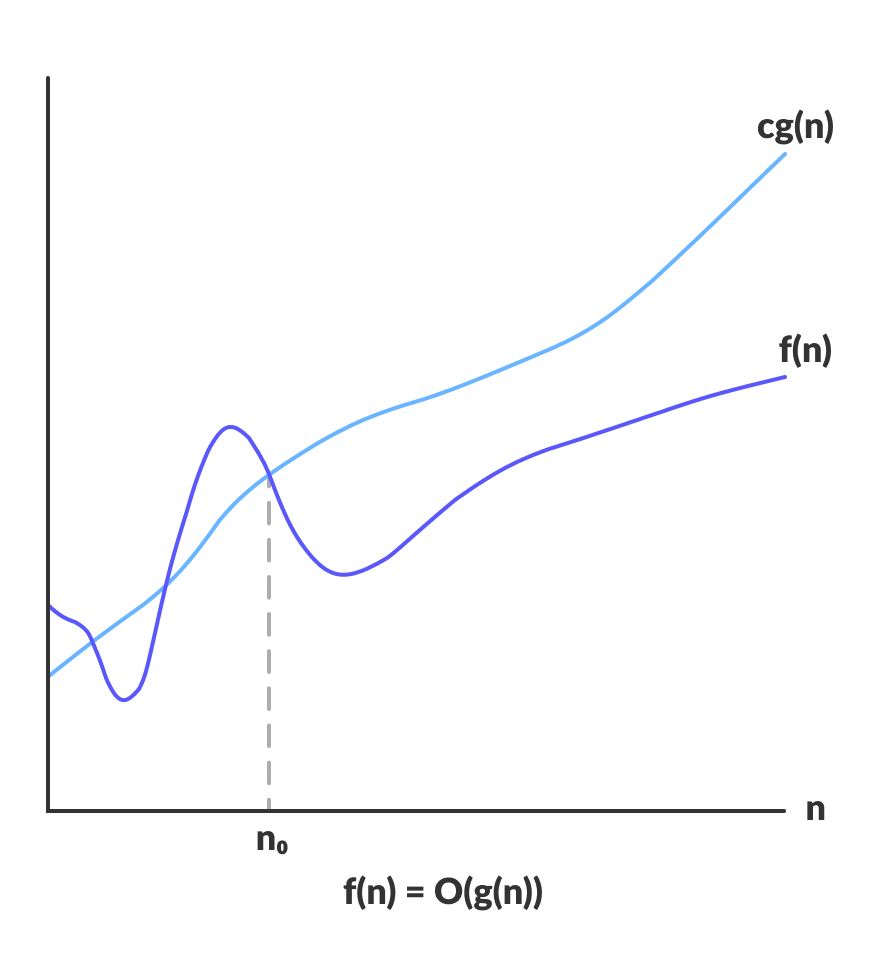
O(g(n)) = { f(n): there exist positive constants c and n0 such that 0 ≤ f(n) ≤ cg(n) for all n ≥ n0 }
Der obige Ausdruck kann als eine Funktion f(n) beschrieben werden gehört zur Menge O(g(n)), wenn es eine positive Konstante c gibt, so dass sie zwischen 0 und cg(n) liegt, für ausreichend große n.
Für jeden Wert von n überschreitet die Laufzeit eines Algorithmus nicht die von O(g(n)) angegebene Zeit.
Da sie die Worst-Case-Laufzeit eines Algorithmus angibt, wird sie häufig zur Analyse eines Algorithmus verwendet, da wir immer am Worst-Case-Szenario interessiert sind.
Omega-Notation (Ω-Notation)
Die Omega-Notation stellt die untere Grenze der Laufzeit eines Algorithmus dar. Sie liefert also die Best-Case-Komplexität eines Algorithmus.

Ω(g(n)) = { f(n): there exist positive constants c and n0 such that 0 ≤ cg(n) ≤ f(n) for all n ≥ n0 }
Der obige Ausdruck kann als eine Funktion beschrieben werden f(n) gehört zur Menge Ω(g(n)), wenn es eine positive Konstante c gibt, so dass sie über cg(n) liegt, für ausreichend große n.
Für jeden Wert von n ist die minimale Zeit, die der Algorithmus benötigt, durch Omega Ω(g(n)) gegeben.
Theta-Notation (Θ-Notation)
Die Theta-Notation umschließt die Funktion von oben und unten. Da sie die obere und untere Schranke der Laufzeit eines Algorithmus darstellt, wird sie zur Analyse der durchschnittlichen Komplexität eines Algorithmus verwendet.
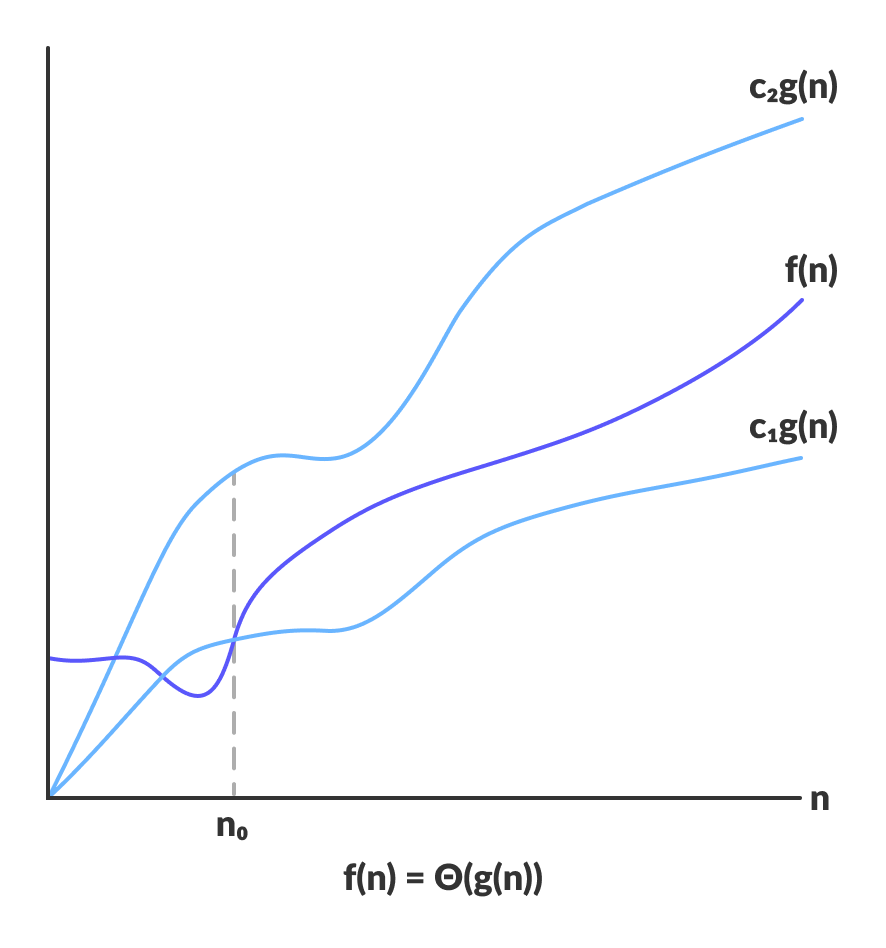
Für eine Funktion g(n) ist Θ(g(n)) durch die Beziehung gegeben:
Θ(g(n)) = { f(n): there exist positive constants c1, c2 and n0 such that 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n) for all n ≥ n0 }
Der obige Ausdruck kann als eine Funktion f(n) beschrieben werden, die zur Menge Θ(g(n)) gehört, wenn es gibt positive Konstanten c1 und c2 gibt, so dass es zwischen c1g(n) und c2g(n) eingeordnet werden kann, für ausreichend großes n.
Wenn eine Funktion f(n) irgendwo zwischen c1g(n) und c2g(n) für alle n ≥ n0 liegt, dann wird f(n) als asymptotisch eng begrenzt bezeichnet.