
Ich will ehrlich sein. Ich beschäftige mich schon seit mehr Jahren mit ernsthaftem Rechenkram, als ich zugeben möchte. Manchmal muss man in der Physik einfach Dinge integrieren. Das passiert einfach.
Als ich jedoch meinem Sohn in seinem Mathekurs half, wurde mir klar – was zum Teufel ist mit der Integration los? Ich habe das Gefühl, dass ich ein wirklich solides Verständnis von Ableitungen habe – aber die Integration hat ein paar seltsame Dinge.
Nun, man wird die Dinge nie verstehen, bis man sie in ihre grundlegenden Teile zerlegt. Also, das ist es, was ich tun werde. Ich werde die Fläche unter einer Kurve auf drei verschiedene Arten finden.
Fläche unter Verwendung der Summenschreibweise
Dies ist am einfachsten zu verstehen, aber am schwierigsten zu berechnen. Oh, Moment! Warum finden wir die Fläche unter einer Kurve? OK, warten Sie – mein Beispiel am Ende sollte helfen.
So, die Grundidee ist, eine Fläche in N Rechtecke zu zerlegen (wobei N einfach irgendeine Zahl ist). Ich kann dann die Fläche jedes Rechtecks finden und sie addieren, um die Gesamtfläche zu erhalten. Je mehr Teile ich zerlege, desto besser ist die Antwort – also werde ich einen Ausdruck für diese Fläche schreiben und den Grenzwert nehmen, wenn die Anzahl der Teile gegen unendlich geht.

Die Fläche würde sich dann wie folgt berechnen:
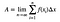
Danach kommt eine Menge Zeug – und es wird ein bisschen langweilig. Sie MÜSSEN das aber durchgehen, um das Ganze zu verstehen. Hier ist ein Video, in dem ich Sie da durchführe.
Wenn Sie eine Funktion verwenden:
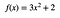
Die Fläche von x = 1 bis x =2 ist 9 (was auch immer die Einheiten sein sollen – ich bin kein Mathematiker, daher stört es mich, die Einheiten wegzulassen).
Fläche mit Anti-Derivaten
Es gibt einen Trick. Es ist ein genialer Trick. Man kann die Fläche unter einer Kurve als bestimmtes Integral schreiben (wobei das Integral eine unendliche Summe von unendlich kleinen Stücken ist – genau wie die Summationsschreibweise).
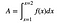
Nun zum verrückten Zeug. VERRÜCKT. Es stellt sich heraus, dass die Fläche die Anti-Ableitung von f(x) ist. Wenn Sie einen Moment innehalten, werden Sie sehen, dass das wild ist. Verrückt wild. Wenn die Ableitung etwas über die Steigung einer Kurve aussagt, sagt das Gegenteil der Ableitung etwas über die Fläche unter der Kurve aus?
Ja. Das ist der fundamentale Satz der Infinitesimalrechnung. Hier ist meine Erklärung (ja, es wird einen Haufen Videos in diesem Beitrag geben und Sie sind VERPFLICHTET, sie alle anzuschauen.
Eigentlich gibt es hier noch eine weitere wichtige Sache. Das definite Integral von x = 1 nach x =2 ist die Differenz der Flächenfunktion A(2) und A(1). Ich werde nicht auf die Details eingehen, weil ich immer noch von der Sache mit der Anti-Ableitung überwältigt bin.
Aber hier ist die Fläche unter der GLEICHEN Funktion, aber mit Integration.
Ja. Sie erhalten das gleiche Endergebnis. Fläche = 9 Hühner² (ich habe die Flächeneinheiten hinzugefügt).
Fläche mit numerischen Berechnungen
Jetzt kommen wir zu den lustigen Sachen. Was wäre, wenn ich die Fläche unter einer Kurve finden würde, indem ich die Fläche eines Haufens von Rechtecken addiere? Oh, warten Sie … das habe ich schon bei der ersten Methode gemacht. Aber wie wäre es damit – ich mache nicht eine unendliche Anzahl von Rechtecken, ich mache einfach eine große Anzahl von Rechtecken? Das ist genau das, worum es bei einer numerischen Berechnung geht.
Natürlich, wenn ich eine Fläche in 100 Teile zerlege, muss ich 100 Sätze von Flächenberechnungen durchführen. Möchte das wirklich jemand tun? Nein – niemand denkt, dass das Spaß machen würde. Aber wissen Sie, wem das egal ist? Computer (elektronische Computer).
Ja, wir können einen Computer dazu bringen, diese Reihe von Berechnungen durchzuführen. Wir müssen ihm nur ein paar Anweisungen geben und dann wird er loslegen und seine Arbeit erledigen. Er wird großartig sein. Hier ist das Grundrezept, das er verwenden wird.
- Bestimmen Sie, in wie viele Stücke Sie die Kurve zerlegen wollen. Wie wäre es mit 100? Mit diesem und dem Start- und End-x-Wert können Sie die Breite jedes Rechtecks berechnen (Δx).
- Setzen Sie die Fläche auf Null (Hühner²). Wir werden immer wieder zu diesem Wert addieren, aber irgendwo muss er ja anfangen.
- Beginnen Sie mit dem anfänglichen x-Wert (in meinem Beispiel ist das x = 1).
- Berechnen Sie die Höhe des Rechtecks. Das wäre f(x) beim aktuellen x-Wert.
- Ermitteln Sie die Fläche dieses Rechtecks und addieren Sie sie zur Gesamtfläche.
- Bewegen Sie sich auf den nächsten x-Wert und wiederholen Sie den Vorgang, bis Sie beim endgültigen x-Wert angelangt sind.
Das ist so einfach, dass es sogar ein Computer machen könnte. OK, ich mache nur Spaß. Einige meiner besten Freunde sind Computer.
Hier ist der Code für diese Berechnung in Python (hier ist ein Link zum eigentlichen Code).
def f(t):
return(3*t**2+2)N=100x1=1
x2=2dx=(x2-x1)/N
A=0
x=x1
while x<=x2:
dA=f(x)*dx
A=A+dA
x=x+dx
print("A = ",A)
Bei N = 100 erhalte ich eine Fläche von 8,95505 – das sind nicht genau 9 Hühner², aber es ist verdammt nah dran. Nahe genug für die meisten Berechnungen von quadratischen Hühnern.
Nur ein paar kurze Kommentare zu diesem Code.
- Ich dachte, es wäre lustig, die Funktion zu einer echten Python-Funktion zu machen (das ist der
def f(t):Teil. - Ich berechne zuerst die Fläche des kleinen Rechtecks (dA) und addiere sie dann zur Gesamtfläche.
- Diese Methode hat tatsächlich Rechtecke, die mit der Funktion auf der linken Seite der Oberseite des Rechtecks aufgereiht sind. Man könnte es auch mit der rechten Seite machen.
- Dazu habe ich auch ein Video gemacht. Aber Sie müssen es sich nicht ansehen – ich habe es größtenteils schon hier erklärt.
Was ist, wenn Sie keine mathematische Funktion haben?
Lassen Sie mich Sie in folgende Situation versetzen. Sie sitzen in einem fahrenden Auto und können NUR den Tacho sehen. Sie notieren sich jede Sekunde den Geschwindigkeitswert (weil Sie ein superschneller Mitschreiber sind). Irgendwann hält das Auto an und Sie müssen herausfinden, wie weit Sie gefahren sind.
Hier ist so etwas (unter Verwendung eines Vernier-Wagens mit einem Bewegungssensor – aber Sie bekommen die Idee, dass dies dasselbe ist wie ein tatsächliches Auto).

OK – Achtung, ich werde hier schummeln. Die Vernier-Spur sammelt Positionsdaten, die auf diesen Linien auf der Spur basieren. Aus den Positionsdaten errechnet er die Geschwindigkeit. Ich habe also bereits die Position des Wagens – aber tun wir mal so, als würde er nur die Geschwindigkeit als Funktion der Zeit angeben. Dann würde es etwa so aussehen.

Sehen Sie. Das ist keine Funktion – das ist eine Raumstation. Nein, warte – das ist aus Star Wars. Aber trotzdem ist es keine mathematische Funktion. Es sind nur Daten. Man kann die Anti-Ableitung von Daten nicht finden (naja, nicht mit den normalen Regeln und so). Aber halt! Die numerische Integration funktioniert ganz gut.
Natürlich gibt es hier noch etwas anderes Wichtiges. Es ist die Idee, dass der Bereich unter dieser Kurve etwas Reales repräsentiert. Stellen Sie sich vor, Sie hätten ein Auto, das sich mit einer konstanten Geschwindigkeit für eine gewisse Zeit bewegt. Sie könnten die Auslenkung ziemlich einfach berechnen:
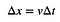
Wenn Sie ein Diagramm der Geschwindigkeit gegen die Zeit haben. Zeit, würde diese konstante Geschwindigkeit wie ein Rechteck aussehen. Ja, die Fläche dieses Rechtecks wäre v*Δt. Wenn es sich NICHT um eine konstante Geschwindigkeit handelt, wäre die Fläche unter dem Geschwindigkeits-Zeit-Diagramm immer noch die Verschiebung.
OK, ein letztes Video. Hier ist meine Erklärung der Codierung, um dieses Verschiebungsproblem zu lösen.
Schauen Sie sich unbedingt alle Videos an.